[GoogleMap] 表示のしくみ

2016-08-29

オンライン地図表示のしくみ

Google Map、Open Streat map。世の中にはいろいろな地図がある。これらの地図の多くは、小さな正方形の地図画像を並べて敷きつめることによって大きな地図を表示している。とまあ、このようなことは今更記事にしなくても調べればわかる話ではあるのだけど。しかし、今後このブログで書くであろう地図に関する記事の前準備としてメモの意味合いもこめて書いておきたいなあと思う。

小さな地図 256×256ピクセルのタイル

世の中にあるいろいろな地図。そのうち少なくともgoogle mapとOpen streat mapは、小さな256×256ピクセルの正方形の画像を並べて表示することで大きな地図を表示している。最も縮小表示した地図。それは、256×256の小さな画像の中に世界が収まっている。画像の中心、つまり世界の中心は緯度、経度共に0度となっており、ちょうど下記のような画像になる。

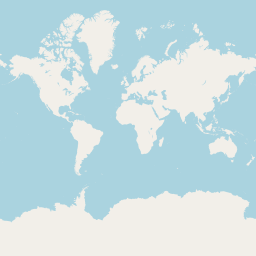_{※画像はopenstreetmap.orgのものを掲載しています。}

もう一段階地図を拡大してみよう。今度は、先ほどの画像の左上の１／４の世界がちょうど256×256ピクセルの正方形の画像に収まっている。世界の中心、緯度、経度共に0度は下記画像の右下の角になる。

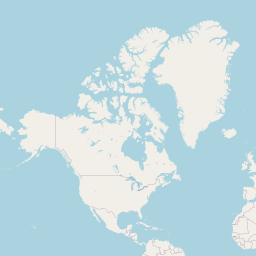_{※画像はopenstreetmap.orgのものを掲載しています。}

このようにして、地図を一段階拡大するたびに、地図は1/1、1/4、1/16・・、のように細かく分割されていく。このどれだけ拡大したかをズームレベルと呼んでいる。そして世界が256×256の画像に収まった時のズームレベルを０、1/4の時、つまり４つに分かれた時をズームレベル１のようにして、ズームレベルは１ずつ増えていく。

最大のズームレベル、それは？？

地図の画像数(分割数)が１つの時はズームレベル０。４つの時はズームレベル１。１６の時はズームレベル２。このズームレベル２までの法則を考えると、どうやら画像の分割数は４のズームレベル乗で計算できるようだ。

$$4^0＝1$$
$$4^1＝4$$
$$4^2＝16$$
$$4^3＝64$$

$$4^{10}＝1048576$$

$$4^{18}＝68719476736$$ ろっぴゃくはちじゅうななおく！
$$4^{19}＝274877906944$$ に、にせんななひゃくおくー！
$$4^{20}＝1.0995116e+12$$ ???

google先生に計算してもらったところ、20乗になったところでe+とか人間の話せない言葉で回答されてしまいました。で、実際のところズームレベルは19が最大のようである。この分割数で大阪駅を表示した所、下記のようになる。これ以上必要ないぐらいに十分に拡大されてると思う。

_{※画像はopenstreetmap.orgのものを掲載しています。}

どの画像を表示するか？

先ほどの例だと、ズームレベル１９では約2700億個の画像に世界はバラバラに分割されてしまう。このバラバラの画像の中から一体どの画像を選べば目的の画像を表示できるのだろう？少し難しいが、少しだけ数学の時間である。みんなだいすき三角関数も出てくる。

タイルの番号

さて、数学の時間の前に。ズームレベル２の時、つまり世界が１６個に分割されてしまった場合を例に少し話をしたいと思う。16個に分割の場合、世界は４×４に並べて表示されることになる。このように並べて敷きつめることから、１つ１つの地図画像をタイルと呼んだりする。そしてこのタイルには番号が付けられている。左上のタイルを0-0番。その右を1-0番。その右を2-0番。0-0番の下は0-1番。その下は0-2番といったようになる。番号はそれぞれ、経度、緯度から求めることができる。

経度から経度方向のタイル番号を計算する

google map、Open streat mapなどの地図では、経度は東経をプラス、西経をマイナスで表す。つまり、-180度〜180度のようになる(細かく言うと、-180度と180度は同じなので、-180 <= x < 180となる)。この-180度〜180度の値から、経度方向のタイル番号を計算してみる。経度方向の計算は少し簡単で三角関数は出てこない。

ズームレベル0の場合、-180〜180度の世界が1つに分割されている。なので、求めるタイル番号は経度が何であっても0になる。
ズームレベル1の場合、-180〜180度の世界が2つに分割されている。なので、求めるタイル番号は-180度から0度より小さい場合に0、0度から180度より小さい場合に1となる。
ズームレベル2の場合、-180〜180度の世界が4つに分割されている。なので、求めるタイル番号は-180度から-90度より小さい場合に0、-90度から0度より小さい場合に1となる。(以下略)

このようにして、ズームレベルに応じて-180〜180度の世界が幾つに分割されるか、からタイルの番号がわかる。式で書くと下記のようになる。

$$経度のタイル番号 = \frac{経度 + 180}{360} \times 2 ^ {zoom}$$

javascriptの関数だと下記のようになる。

1// lng: -180<=lng<180
2// zoom: 0~19
3var lngToTile = function(lng, zoom){
4    return ((lng + 180.0) / 360.0) * Math.pow(2, zoom);
5};

緯度から緯度方向のタイル番号を計算する

緯度方向のタイル番号については、数式を見ても「お、おぅ・・」としか言えないぐらいよくわからない。メルカトル図法というのは見たことがあると思うが、北極や南極に近づくに従って地図が間延びしているあれである。このどれ位間延びしているのかを表す式があるのだが、ネットで探した所下記に詳しく書いてあった。(なるほど、わからん・・。)

メルカトル図法

とにかく、緯度に対してどれだけ地図が歪むかの式は下記のようである。

$$y = \frac{\log(\tan(\frac{\pi}{4} + \frac{緯度}{2}))}{\pi}$$

これをグラフに書くと下記のようになる。

このグラフは、わざとyの範囲を-1〜1の間に絞ってある。というのも、緯度90度、-90度で計算すると結果が∞になるためである。また、google map、Open streat mapなどの地図では、ズームレベル０の場合にこの-1〜1の範囲が256ピクセルに収まるようにして、世界を正方形に保とうとしている。上記の式から、yが-1と1になる時の緯度を求めると、下記のようになる(この式は先程の逆関数だが、やはり難しい・・)。

$$\frac{(2 \arctan(e ^ \pi) - \frac{\pi}{2}) \times 180}{\pi} = 85.051128779806589$$

$$\frac{(2 \arctan(e ^ {-\pi}) - \frac{\pi}{2}) \times 180}{\pi} = -85.051128779806589$$

つまり、ネット上の地図は北緯、南緯ともに85.051128779806589度以上の場所を切り捨てて、世界を表示している。

この歪みを考慮して、ズームレベルにより世界が幾つに分割されるかを求めると、緯度方向のタイルの番号がわかる。式で書くと下記のようになる(下記の式は、-1〜1の範囲が1〜0の範囲になるように調整したものに、ズームレベルによる分割数を掛けている)。

$$緯度のタイル番号 = \frac{(1 - \frac{\log(\tan(\frac{\pi}{4} + \frac{緯度}{2}))}{\pi})}{2} \times 2 ^ {zoom}$$

javascriptの関数だと下記のようになる。

1// lat: -85.0511<=lat<85.0511
2// zoom: 0~19
3var latToTile = function(lat, zoom){
4    return (1.0 - Math.log(Math.tan(lat * Math.PI / 360.0 + Math.PI / 4)) / Math.PI) / 2 * Math.pow(2, zoom);
5};

大阪駅を表示してみる

タイル番号計算

先程も表示した大阪駅。大阪駅を例にタイル番号を計算し表示してみる。大阪駅の座標は緯度34.702485、経度135.495951である。ズームの16で計算してみる。

経度のタイル番号 $$\frac{135.495951 + 180.0}{360.0} \times 2 ^ {16} ≒ 57434$$
緯度のタイル番号 $$y = \frac{\log(\tan(\frac{\pi}{4} + \frac{34.702485}{2}))}{\pi} = 0.20579021686571844$$ $$\frac{1 - y}{2} \times 2 ^ {16} ≒ 26024$$

表示

open streat mapの場合、http://tile.openstreetmap.org/zoom/経度のタイル番号/緯度のタイル番号.pngでそのタイルを表示できる。つまり、大阪駅は<img src="http://tile.openstreetmap.org/16/57434/26024.png">となる。

_{※画像はopenstreetmap.orgのものを掲載しています。}